ngraph.path/README.md

# ngraph.path

Fast path finding for arbitrary graphs. [Play with a demo](https://anvaka.github.io/ngraph.path.demo/) or [watch it](https://www.youtube.com/watch?v=hGeZuIEV6KU) on YouTube.

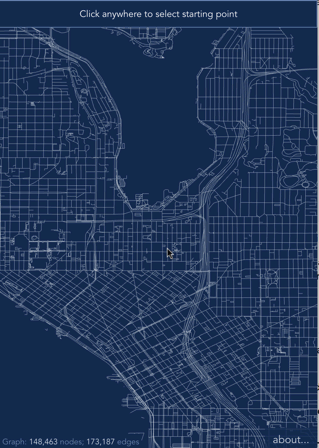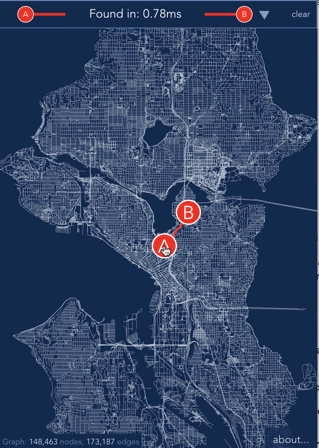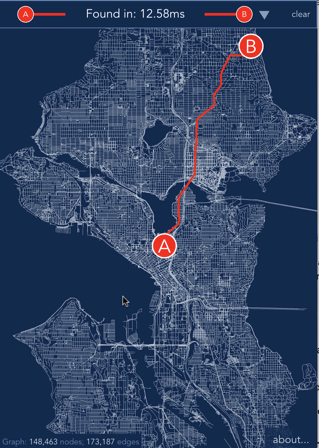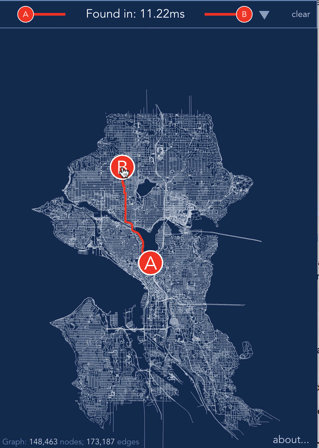[![demo](https://raw.githubusercontent.com/anvaka/ngraph.path/master/docs/seattle.gif)](https://anvaka.github.io/ngraph.path.demo/)

If you want to learn how the demo was made, please refer to the [demo's source code](https://github.com/anvaka/ngraph.path.demo#ngraphpath-demo).
I tried to describe it in great details.

# Performance

I measured performance of this library on New York City roads graph (`733,844` edges, `264,346` nodes).
It was done by solving `250` random path finding problems. Each algorithm was solving
the same set of problems. Table below shows required time to solve one problem.

|                                        | Average | Median | Min | Max   | p90   | p99   |
|----------------------------------------|---------|:------:|:---:|-------|-------|-------|
|      A* greedy (suboptimal)            |   32ms  |  24ms  | 0ms | 179ms |  73ms | 136ms |
|      NBA*                              |   44ms  |  34ms  | 0ms | 222ms | 107ms | 172ms |
|      A*, unidirectional                |   55ms  |  38ms  | 0ms | 356ms | 123ms | 287ms |
|      Dijkstra                          |  264ms  | 258ms  | 0ms | 782ms | 483ms | 631ms |

"A* greedy" converged the fastest, however, as name implies the found path is not necessary
globally optimal.

## Why is it fast?

There are a few things that contribute to the performance of this library.

I'm using heap-based priority queue, built specifically for the path finding.
I [modified a heap's](https://github.com/anvaka/ngraph.path/blob/master/a-star/NodeHeap.js) implementation,
so that changing priority of any element takes `O(lg n)` time.

Each path finder opens many graph nodes during its exploration, which creates pressure
on garbage collector. To avoid the pressure, I've created an [object pool](https://github.com/anvaka/ngraph.path/blob/master/a-star/nba/makeNBASearchStatePool.js),
which recycles nodes when possible.

In general, the `A*` algorithm helps to converge to the optimal solution faster than
Dijkstra, because it uses "hints" from the heuristic function. When search is performed
in both directions (`source -> target` and `target -> source`), the convergence can be
improved even more. The [NBA*](https://github.com/anvaka/ngraph.path/blob/master/a-star/nba/index.js) algorithm
is a bi-directional path finder, that guarantees optimal shortest path. At the same time it
removes balanced heuristic requirement. It also seem to be the fastest algorithm, among implemented 
here *(NB: If you have suggestions how to improve this even further - please let me know!)*

I also tried to create my own version of bi-directional A* search, which
turned out to be harder than I expected - the two searches met each other quickly, but the point
where they met was not necessary on the shortest global path. It was close to optimal, but not the optimal.
I wanted to remove the code, but then changed my mind: It finds a path very quickly. So, in case when
speed matters more than correctness, this could be a good trade off. I called this algorithm `A* greedy`,
but maybe it should be `A* lazy`.

# usage

## installation

You can install this module, bu requiring it from npm:

```
npm i ngraph.path
```

Or download from CDN:

``` html
<script src='https://unpkg.com/ngraph.graph@1.1.0/dist/ngraph.path.min.js'></script>
```

If you download from CDN the library will be available under `ngraphPath` global name.

## Basic usage

This is a basic example, which finds a path between arbitrary
two nodes in arbitrary graph

``` js
let path = require('ngraph.path');
let pathFinder = path.aStar(graph); // graph is https://github.com/anvaka/ngraph.graph

// now we can find a path between two nodes:
let fromNodeId = 40;
let toNodeId = 42;
let foundPath = pathFinder.find(fromNodeId, toNodeId);
// foundPath is array of nodes in the graph
```

Example above works for any graph, and it's equivalent to unweighted [Dijkstra's algorithm](https://en.wikipedia.org/wiki/Dijkstra%27s_algorithm).

## Weighted graph

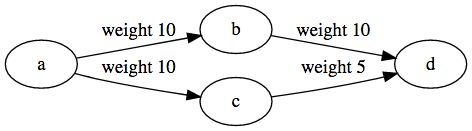
Let's say we have the following graph:

``` js
let createGraph = require('ngraph.graph');
let graph = createGraph();

graph.addLink('a', 'b', {weight: 10});
graph.addLink('a', 'c', {weight: 10});
graph.addLink('c', 'd', {weight: 5});
graph.addLink('b', 'd', {weight: 10});
```

![weighted](https://raw.githubusercontent.com/anvaka/ngraph.path/master/docs/weighted.png)

We want to find a path with the smallest possible weight:

``` js
let pathFinder = aStar(graph, {
  // We tell our pathfinder what should it use as a distance function:
  distance(fromNode, toNode, link) {
    // We don't really care about from/to nodes in this case,
    // as link.data has all needed information:
    return link.data.weight;
  }
});
let path = pathFinder.find('a', 'd');
```

This code will correctly print a path: `d <- c <- a`.

## Guided (A-Star)

When pathfinder searches for a path between two nodes it considers all
neighbors of a given node without any preference. In some cases we may want to
guide the pathfinder and tell it our preferred exploration direction.

For example, when each node in a graph has coordinates, we can assume that 
nodes that are closer towards the path-finder's target should be explored 
before other nodes.

``` js
let createGraph = require('ngraph.graph');
let graph = createGraph();

// Our graph has cities:
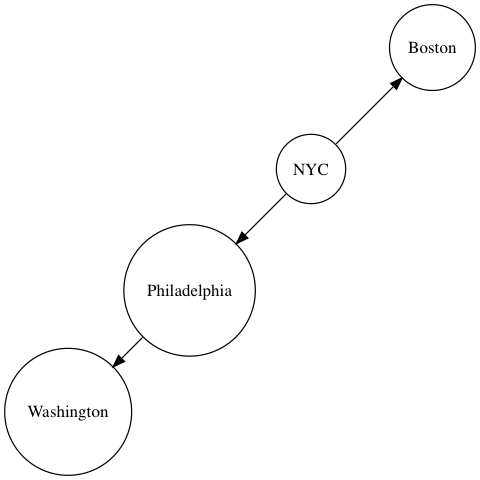
graph.addNode('NYC', {x: 0, y: 0});
graph.addNode('Boston', {x: 1, y: 1});
graph.addNode('Philadelphia', {x: -1, y: -1});
graph.addNode('Washington', {x: -2, y: -2});

// and railroads:
graph.addLink('NYC', 'Boston');
graph.addLink('NYC', 'Philadelphia');
graph.addLink('Philadelphia', 'Washington');
```

![guided](https://raw.githubusercontent.com/anvaka/ngraph.path/master/docs/guided.png)

When we build the shortest path from NYC to Washington, we want to tell the pathfinder
that it should prefer Philadelphia over Boston.

``` js
let pathFinder = aStar(graph, {
  distance(fromNode, toNode) {
    // In this case we have coordinates. Lets use them as
    // distance between two nodes:
    let dx = fromNode.data.x - toNode.data.x;
    let dy = fromNode.data.y - toNode.data.y;

    return Math.sqrt(dx * dx + dy * dy);
  },
  heuristic(fromNode, toNode) {
    // this is where we "guess" distance between two nodes.
    // In this particular case our guess is the same as our distance
    // function:
    let dx = fromNode.data.x - toNode.data.x;
    let dy = fromNode.data.y - toNode.data.y;

    return Math.sqrt(dx * dx + dy * dy);
  }
});
let path = pathFinder.find('NYC', 'Washington');
```

With this simple heuristic our algorithm becomes smarter and faster.

It is very important that our heuristic function does not overestimate actual distance
between two nodes. If it does so, then algorithm cannot guarantee the shortest path.

## oriented graphs

If you want the pathfinder to treat your graph as oriented - pass `oriented: true` setting:

``` js
let pathFinder = aStar(graph, {
  oriented: true
});
```

## available finders

The library implements a few A* based path finders:

``` js
let aStarPathFinder = path.aStar(graph, options);
let aGreedyStar = path.aGreedy(graph, options);
let nbaFinder = path.nba(graph, options);
```

Each finder has just one method `find(fromNodeId, toNodeId)`, which returns array of
nodes, that belongs to the found path. If no path exists - empty array is returned.

# Which finder to choose?

With many options available, it may be confusing whether to pick Dijkstra or A*.

I would pick Dijkstra if there is no way to guess a distance between two arbitrary nodes
in a graph. If we can guess distance between two nodes - pick A*.

Among algorithms presented above, I'd recommend `A* greedy` if you care more about speed and
less about accuracy. However if accuracy is your top priority - choose `NBA*`. 
This is a bi-directional, optimal A* algorithm with very good exit criteria. You can read
about it here: https://repub.eur.nl/pub/16100/ei2009-10.pdf

# license

MIT