mirror of
https://github.com/trekhleb/javascript-algorithms.git
synced 2025-12-08 19:06:00 +00:00
97 lines
4.1 KiB
Markdown
97 lines
4.1 KiB
Markdown
# Red–Black Tree
|
||
|
||
_Read this in other languages:_
|
||
[_Português_](README.pt-BR.md)
|
||
|
||
A **red–black tree** is a kind of self-balancing binary search
|
||
tree in computer science. Each node of the binary tree has
|
||
an extra bit, and that bit is often interpreted as the
|
||
color (red or black) of the node. These color bits are used
|
||
to ensure the tree remains approximately balanced during
|
||
insertions and deletions.
|
||
|
||
Balance is preserved by painting each node of the tree with
|
||
one of two colors in a way that satisfies certain properties,
|
||
which collectively constrain how unbalanced the tree can
|
||
become in the worst case. When the tree is modified, the
|
||
new tree is subsequently rearranged and repainted to
|
||
restore the coloring properties. The properties are
|
||
designed in such a way that this rearranging and recoloring
|
||
can be performed efficiently.
|
||
|
||
The balancing of the tree is not perfect, but it is good
|
||
enough to allow it to guarantee searching in `O(log n)` time,
|
||
where `n` is the total number of elements in the tree.
|
||
The insertion and deletion operations, along with the tree
|
||
rearrangement and recoloring, are also performed
|
||
in `O(log n)` time.
|
||
|
||
An example of a red–black tree:
|
||
|
||

|
||
|
||
## Properties
|
||
|
||
In addition to the requirements imposed on a binary search
|
||
tree the following must be satisfied by a red–black tree:
|
||
|
||
- Each node is either red or black.
|
||
- The root is black. This rule is sometimes omitted.
|
||
Since the root can always be changed from red to black,
|
||
but not necessarily vice versa, this rule has little
|
||
effect on analysis.
|
||
- All leaves (NIL) are black.
|
||
- If a node is red, then both its children are black.
|
||
- Every path from a given node to any of its descendant
|
||
NIL nodes contains the same number of black nodes.
|
||
|
||
Some definitions: the number of black nodes from the root
|
||
to a node is the node's **black depth**; the uniform
|
||
number of black nodes in all paths from root to the leaves
|
||
is called the **black-height** of the red–black tree.
|
||
|
||
These constraints enforce a critical property of red–black
|
||
trees: _the path from the root to the farthest leaf is no more than twice as long as the path from the root to the nearest leaf_.
|
||
The result is that the tree is roughly height-balanced.
|
||
Since operations such as inserting, deleting, and finding
|
||
values require worst-case time proportional to the height
|
||
of the tree, this theoretical upper bound on the height
|
||
allows red–black trees to be efficient in the worst case,
|
||
unlike ordinary binary search trees.
|
||
|
||
## Balancing during insertion
|
||
|
||
### If uncle is RED
|
||
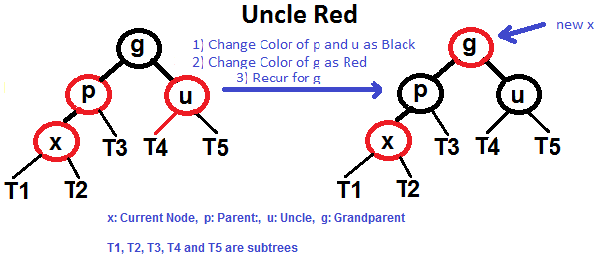
|
||
|
||
### If uncle is BLACK
|
||
|
||
- Left Left Case (`p` is left child of `g` and `x` is left child of `p`)
|
||
- Left Right Case (`p` is left child of `g` and `x` is right child of `p`)
|
||
- Right Right Case (`p` is right child of `g` and `x` is right child of `p`)
|
||
- Right Left Case (`p` is right child of `g` and `x` is left child of `p`)
|
||
|
||
#### Left Left Case (See g, p and x)
|
||
|
||
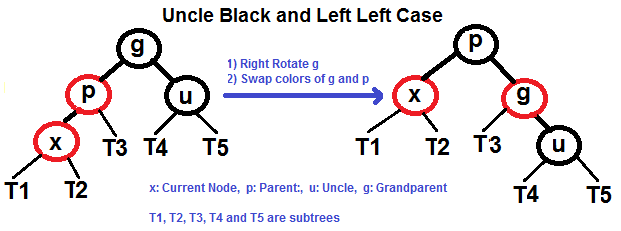
|
||
|
||
#### Left Right Case (See g, p and x)
|
||
|
||
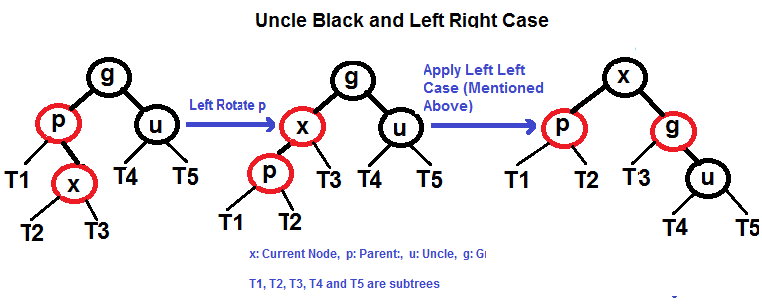
|
||
|
||
#### Right Right Case (See g, p and x)
|
||
|
||
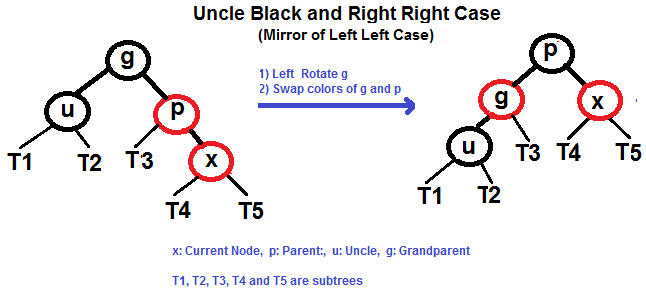
|
||
|
||
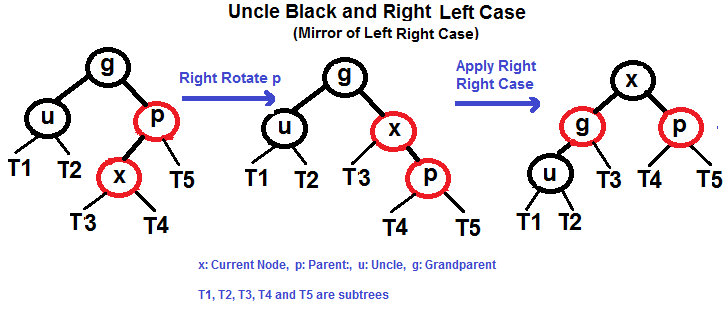
#### Right Left Case (See g, p and x)
|
||
|
||
|
||
|
||
## References
|
||
|
||
- [Wikipedia](https://en.wikipedia.org/wiki/Red%E2%80%93black_tree)
|
||
- [Red Black Tree Insertion by Tushar Roy (YouTube)](https://www.youtube.com/watch?v=UaLIHuR1t8Q&list=PLLXdhg_r2hKA7DPDsunoDZ-Z769jWn4R8&index=63)
|
||
- [Red Black Tree Deletion by Tushar Roy (YouTube)](https://www.youtube.com/watch?v=CTvfzU_uNKE&t=0s&list=PLLXdhg_r2hKA7DPDsunoDZ-Z769jWn4R8&index=64)
|
||
- [Red Black Tree Insertion on GeeksForGeeks](https://www.geeksforgeeks.org/red-black-tree-set-2-insert/)
|
||
- [Red Black Tree Interactive Visualisations](https://www.cs.usfca.edu/~galles/visualization/RedBlack.html)
|