let path = require('ngraph.path');
let pathFinder = path.aStar(graph);

// now we can find a path between two nodes:
let fromNodeId = 40;
let toNodeId = 42;
let foundPath = pathFinder.find(fromNodeId, toNodeId);
// foundPath is array of nodes in the graph

Example above works for any graph, and it's equivalent to unweighted Dijkstra's algorithm.

Weighted graph

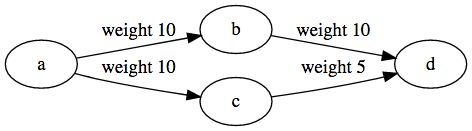
Let's say we have the following graph:

let createGraph = require('ngraph.graph');
let graph = createGraph();

graph.addLink('a', 'b', {weight: 10});
graph.addLink('a', 'c', {weight: 10});
graph.addLink('c', 'd', {weight: 5});
graph.addLink('b', 'd', {weight: 10});

We want to find a path with the smallest possible weight:

let pathFinder = aStar(graph, {
  // We tell our pathfinder what should it use as a distance function:
  distance(fromNode, toNode, link) {
    // We don't really care about from/to nodes in this case,
    // as link.data has all needed information:
    return link.data.weight;
  }
});
let path = pathFinder.find('a', 'd');

This code will correctly print a path: d <- c <- a.

Guided (A-Star)

When pathfinder searches for a path between two nodes it considers all neighbors of a given node without any preference. In some cases we may want to guide the pathfinder and tell it our preferred exploration direction.

For example, when each node in a graph has coordinates, we can assume that nodes that are closer towards the path-finder's target should be explored before other nodes.

let createGraph = require('ngraph.graph');
let graph = createGraph();

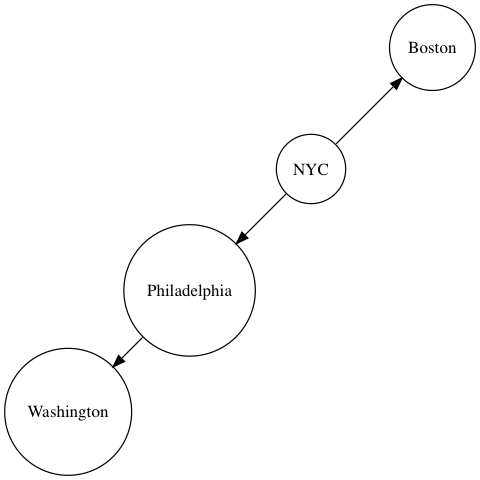
// Our graph has cities:
graph.addNode('NYC', {x: 0, y: 0});
graph.addNode('Boston', {x: 1, y: 1});
graph.addNode('Philadelphia', {x: -1, y: -1});
graph.addNode('Washington', {x: -2, y: -2});

// and railroads:
graph.addLink('NYC', 'Boston');
graph.addLink('NYC', 'Philadelphia');
graph.addLink('Philadelphia', 'Washington');

When we build the shortest path from NYC to Washington, we want to tell the pathfinder that it should prefer Philadelphia over Boston.

let pathFinder = aStar(graph, {
  distance(fromNode, toNode) {
    // In this case we have coordinates. Lets use them as
    // distance between two nodes:
    let dx = fromNode.data.x - toNode.data.x;
    let dy = fromNode.data.y - toNode.data.y;

    return Math.sqrt(dx * dx + dy * dy);
  },
  heuristic(fromNode, toNode) {
    // this is where we "guess" distance between two nodes.
    // In this particular case our guess is the same as our distance
    // function:
    let dx = fromNode.data.x - toNode.data.x;
    let dy = fromNode.data.y - toNode.data.y;

    return Math.sqrt(dx * dx + dy * dy);
  }
});
let path = pathFinder.find('NYC', 'Washington');

With this simple heuristic our algorithm becomes smarter and faster.

It is very important that our heuristic function does not overestimate actual distance between two nodes. If it does so, then algorithm cannot guarantee the shortest path.

Performance

Internally, I'm using heap-based priority queue, built specifically for path finding. I modified it, so that changing priority of any element in the queue takes O(lg n) time.

I measured performance of this implementation on New York City roads graph (733,844 edges, 264,346 nodes). It was done by solving 250 random path finding problems. Each algorithm was solving the same set of problems. Table below shows required time to solve one problem.

	Average	Median	Min	Max	p90	p99
A*, bidirectional (local optima)	32ms	24ms	0ms	132ms	71ms	131ms
A*, bidirectional (global optima)	61ms	48ms	0ms	319ms	133ms	295ms
A*, unidirectional	59ms	39ms	0ms	354ms	137ms	354ms
Dijkstra, unidirectional	272ms	264ms	0ms	733ms	505ms	587ms
Dijkstra, bidirectional (global optima)	269ms	253ms	1ms	668ms	500ms	607ms
Dijkstra, bidirectional (local optima)	158ms	143ms	0ms	441ms	313ms	392ms

"Local optima" in bidirectional search converged the fastest, however, as name implies the found path is not necessary globally optimal. In local optima problems we stop the finder as soon as two searches intersect.

I did implement bidirectional globally optimal finder, but looking at these results I think I might be missing something - I'd like to see better gains on bidirectional search.

Which method to choose?

With many options available, it may be confusing whether to pick Dijkstra or A*.

I would pick Dijkstra if there is no way to guess a distance between two arbitrary nodes in a graph. If we can guess distance between two nodes - pick A*.

license

MIT